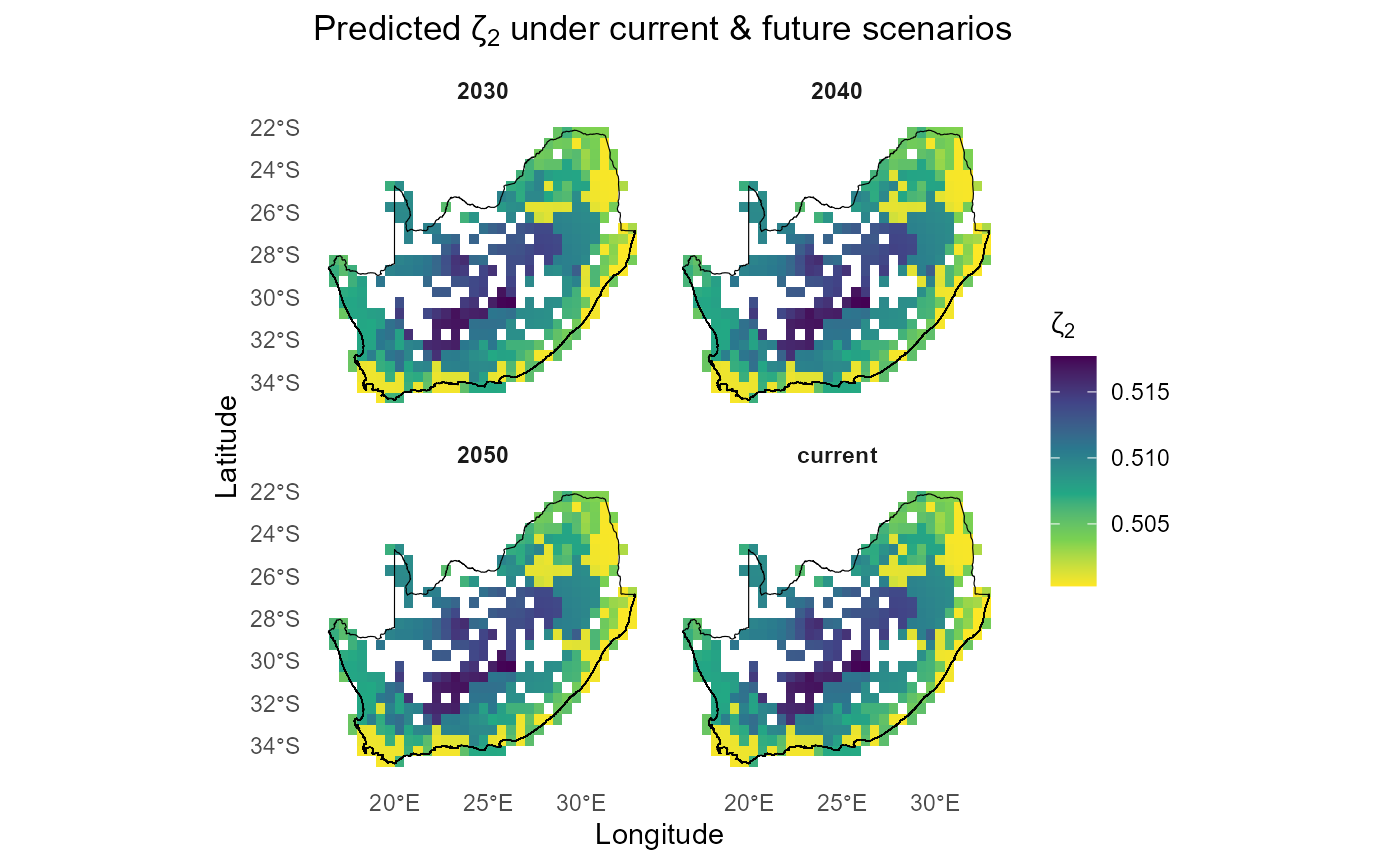dissmapr
A Novel Framework for Automated Compositional Dissimilarity and Biodiversity Turnover Analysis
1. Predict current Zeta Diversity (zeta2) using
predict_dissim()
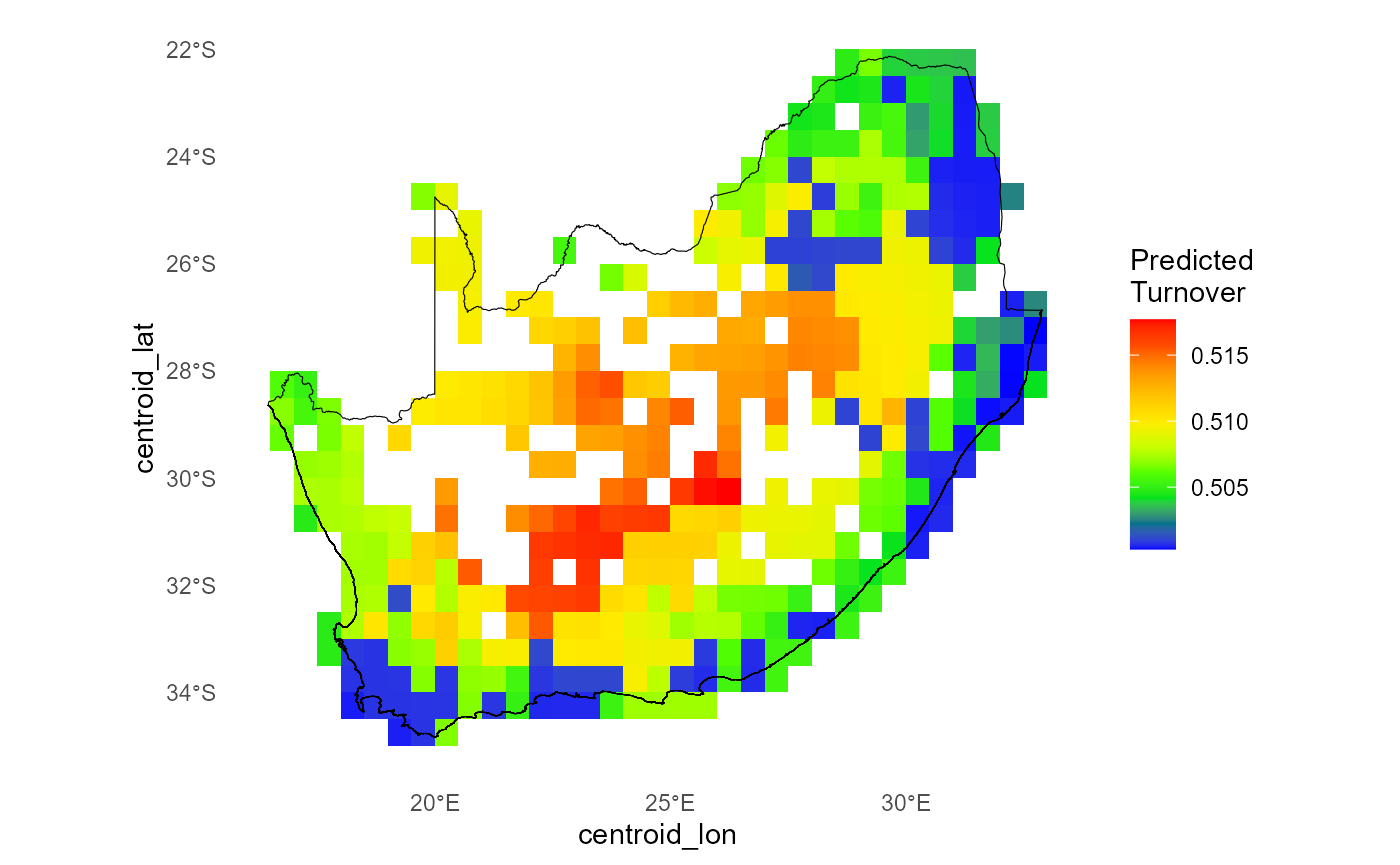
In this step we use our fitted order-2 GDM (zeta2) to
generate a spatial map of pairwise compositional turnover (ζ₂) under
current conditions. By calling predict_dissim() we
- compute each site’s sampling‐effort‐adjusted species richness and
mean distance to all other sites;
- apply the same environmental I-spline transformations used in the
model;
- predict the Jaccard-scaled turnover (ζ₂) on the 0–1 scale;
- optionally plot the resulting heatmap with your study boundary overlaid.
We set a random seed for reproducibility (so Monte Carlo sampling
inside predict_dissim() yields the same results each time),
pull out just the species columns once, then inspect the returned
predictors_df to confirm its dimensions, column names, and
a quick peek at the key model outputs.
# Predict current zeta diversity using `predict_dissim` with sampling effort, geographic distance and environmental variables
# Only non-colinear environmental variables used in `zeta2` model
set.seed(123) # set.seed to generate exactly the same random results i.e. sam=100
spp_cols = names(grid_spp_pa[,-(1:7)])
predictors_df = predict_dissim(
grid_spp = grid_spp_pa,
species_cols = spp_cols,
env_vars = env_vars_reduced,# env_vars_reduced[,-8]
zeta_model = zeta2, # From simple order 2 run above
# zeta_model = ispline_gdm_tab$zeta_gdm_list[[1]], # From list of Zeta.msgdm models
grid_xy = grid_env,
x_col = "centroid_lon",
y_col = "centroid_lat",
bndy_fc = rsa, # Optional feature collection to plot as boundary
show_plot = TRUE
)
# Check results
dim(predictors_df)
#> [1] 415 14
names(predictors_df)
#> [1] "temp_mean" "iso" "temp_wetQ" "temp_dryQ"
#> [5] "rain_dry" "rain_warmQ" "obs_sum" "distance"
#> [9] "richness" "pred_zeta" "pred_zetaExp" "log_pred_zetaExp"
#> [13] "centroid_lon" "centroid_lat"
head(predictors_df[,5:11])
#> rain_dry rain_warmQ obs_sum distance richness pred_zeta pred_zetaExp
#> 1 -1.227648 -0.17604221 -0.2926985 903.0437 2 0.01930100 0.5048251
#> 2 -1.223151 -0.11642238 -0.2340532 915.4655 31 0.02632131 0.5065799
#> 3 -1.154108 0.06618959 -0.2818954 931.1100 10 0.01570100 0.5039252
#> 4 -1.149209 0.38933728 -0.2865253 949.9390 7 0.01506016 0.5037650
#> 5 -1.080356 0.62285852 -0.2880686 971.8672 6 0.01472191 0.5036804
#> 6 -1.048567 0.57126837 -0.1321955 996.7561 76 0.01438702 0.50359672. Predict future Zeta Diversity using
predict_dissim()
Below we expand our workflow to forecast how ζ₂ respond to three extreme climate futures (2030, 2040, 2050) alongside the current scenario.
First, we define and center-scale each future by adding large temperature increments and rainfall multipliers, then bundle them into a named list of four environmental data frames:
# 1. Identify species & env columns
# spp_cols = names(grid_spp_pa)[-(1:7)]
all_vars = names(env_vars_reduced)
temp_vars = grep("^temp", all_vars, value = TRUE)
rain_vars = grep("^rain", all_vars, value = TRUE)
iso_vars = grep("^iso", all_vars, value = TRUE)
obs_var = "obs_sum"
# 2. Extreme future shifts
horizons = c("2030","2040","2050")
mean_delta = list(
temp = c("2030"= +2, "2040"= +4, "2050"= +6),
iso = c("2030"= +0.5,"2040"= +1.0,"2050"= +1.5),
rain = c("2030"= 0.9, "2040"= 0.8, "2050"= 0.7),
effort= c("2030"= 1.3, "2040"= 1.6, "2050"= 2.0)
)
exagg_factor = c("2030"=1.5, "2040"=2.0, "2050"=2.5)
# 3) helper to amplify deviation from the mean
amplify = function(x, factor) {
m = mean(x, na.rm=TRUE)
m + (x - m) * factor
}
# # 4. Save original scaling parameters
# sc_params = scale(env_vars_reduced)
# mu = attr(sc_params, "scaled:center")
# sigma = attr(sc_params, "scaled:scale")
# 4. Build list of future env tibbles
env_scenarios = c(
list(current = env_vars_reduced),
map(horizons, function(yr) {
df = env_vars_reduced
# mean shifts
df[temp_vars] = df[temp_vars] + mean_delta$temp[yr]
df[iso_vars] = df[iso_vars] + mean_delta$iso[yr]
df[rain_vars] = df[rain_vars] * mean_delta$rain[yr]
df[[obs_var]] = df[[obs_var]] * mean_delta$effort[yr]
# amplify spatial variation
df[temp_vars] = map_dfc(df[temp_vars], amplify, factor = exagg_factor[yr])
df[iso_vars] = map_dfc(df[iso_vars], amplify, factor = exagg_factor[yr])
# clamp obs_sum
df[[obs_var]] = pmin(pmax(df[[obs_var]], 50), 8000)
df
}) |> set_names(horizons)
)
# names(env_scenarios) = names(horizons)
# 5. Prepend current conditions
# env_scenarios = c(list(current = env_vars_reduced), env_futures)
str(env_scenarios, max.level = 1)
#> List of 4
#> $ current: tibble [415 × 7] (S3: tbl_df/tbl/data.frame)
#> $ 2030 : tibble [415 × 7] (S3: tbl_df/tbl/data.frame)
#> $ 2040 : tibble [415 × 7] (S3: tbl_df/tbl/data.frame)
#> $ 2050 : tibble [415 × 7] (S3: tbl_df/tbl/data.frame)Next, we loop through each scenario, re-apply the original centering
and scaling, and call our predict_dissim() helper to
compute ζ₂. We tag each result with its scenario name and combine them
into one tidy data frame:
set.seed(123)
scenario_dfs = purrr::imap(env_scenarios, ~ {
df = predict_dissim(
grid_spp = grid_spp,
species_cols = spp_cols,
env_vars = .x,
zeta_model = zeta2,
grid_xy = grid_env,
x_col = "centroid_lon",
y_col = "centroid_lat",
skip_scale = FALSE,
show_plot = FALSE
)
df$scenario = .y
df
})
str(scenario_dfs, max.level=1)
#> List of 4
#> $ current:'data.frame': 415 obs. of 15 variables:
#> $ 2030 :'data.frame': 415 obs. of 15 variables:
#> $ 2040 :'data.frame': 415 obs. of 15 variables:
#> $ 2050 :'data.frame': 415 obs. of 15 variables:
# all_preds = bind_rows(scenario_dfs) %>%
# mutate(scenario = factor(scenario, levels = c("current", names(temp_shifts))))
all_preds = bind_rows(scenario_dfs)
head(all_preds)
#> temp_mean iso temp_wetQ temp_dryQ rain_dry rain_warmQ obs_sum
#> 1 1.841044 0.05124962 1.426512 0.5759178 -1.227648 -0.17604221 -0.2926985
#> 2 1.770287 -0.16040417 1.434249 0.5279913 -1.223151 -0.11642238 -0.2340532
#> 3 1.888447 0.23118933 1.406438 0.6828768 -1.154108 0.06618959 -0.2818954
#> 4 2.222843 0.75512585 1.510132 0.9797353 -1.149209 0.38933728 -0.2865253
#> 5 2.424011 1.38701985 1.551582 1.1832058 -1.080356 0.62285852 -0.2880686
#> 6 2.809129 1.80976342 1.766238 1.4127484 -1.048567 0.57126837 -0.1321955
#> distance richness pred_zeta pred_zetaExp log_pred_zetaExp centroid_lon
#> 1 903.0437 3 0.01930100 0.5048251 -0.6835432 28.75
#> 2 915.4655 41 0.02632131 0.5065799 -0.6800731 29.25
#> 3 931.1100 10 0.01570100 0.5039252 -0.6853275 29.75
#> 4 949.9390 7 0.01506016 0.5037650 -0.6856454 30.25
#> 5 971.8672 6 0.01472191 0.5036804 -0.6858133 30.75
#> 6 996.7561 107 0.01438702 0.5035967 -0.6859795 31.25
#> centroid_lat scenario
#> 1 -22.25004 current
#> 2 -22.25004 current
#> 3 -22.25004 current
#> 4 -22.25004 current
#> 5 -22.25004 current
#> 6 -22.25004 currentWe can then quickly compare the spatial ζ₂ surfaces under each future:
ggplot(all_preds,
aes(centroid_lon, centroid_lat, fill = pred_zetaExp)) +
geom_tile() +
facet_wrap(~ scenario, ncol = 2) +
scale_fill_viridis_c(direction = -1, name = expression(zeta[2])) +
geom_sf(data = rsa, fill = NA, color = "black", inherit.aes = FALSE) +
coord_sf() +
labs(x = "Longitude", y = "Latitude",
title = expression("Predicted ζ"[2] * " under current & future scenarios")) +
theme_minimal() +
theme(strip.text = element_text(face = "bold"),
panel.grid = element_blank())